ইউক্লিডীয় ছন্দ

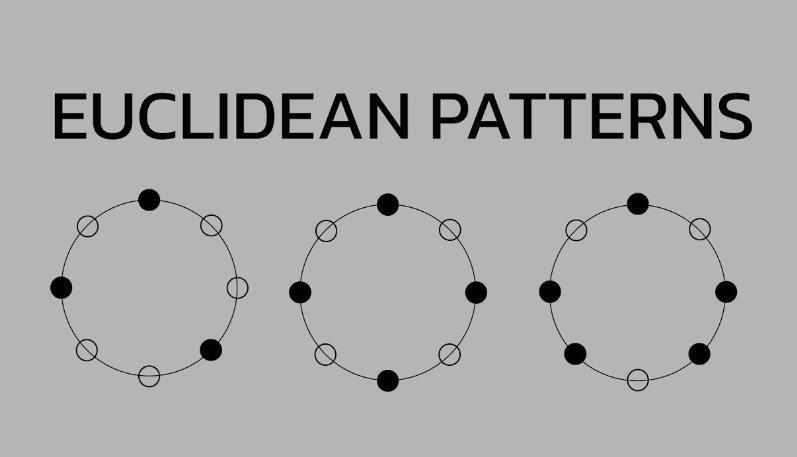
সঙ্গীত এবং গণিতের মধ্যে সংযোগ দীর্ঘকাল পরিচিত, এবং এটি শুধুমাত্র গণিত রক সম্পর্কে নয়। সঙ্গীত, যেমন আগে ব্যাখ্যা করা হয়েছে, একটি দ্বি-মাত্রিক সমতলে আকার তৈরি করতে ব্যবহার করা যেতে পারে, এবং তাল এবং সংখ্যাগুলিও ঘনিষ্ঠভাবে সম্পর্কিত। এই সমন্বয়ের একটি প্রধান উদাহরণ হল ইউক্লিডীয় ছন্দ, যা বাদ্যযন্ত্র এবং গাণিতিক ধারণার মধ্যে সমন্বয় প্রদর্শন করে।

খ্রিস্টপূর্ব 3 য় শতাব্দীতে, প্রাচীন গ্রীক গণিতবিদ ইউক্লিড দুটি সংখ্যার সর্বশ্রেষ্ঠ সাধারণ ভাজক নির্ধারণের জন্য একটি অ্যালগরিদম তৈরি করেছিলেন, একটি ছোট সংখ্যা এবং একটি বড় এবং ছোট সংখ্যার মধ্যে পার্থক্য নিয়ে গঠিত একটি জোড়া সংখ্যার উপর ভিত্তি করে।

2004 সালে, আবু ধাবির নিউ ইয়র্ক বিশ্ববিদ্যালয়ের একজন কানাডিয়ান কম্পিউটার বিজ্ঞানের অধ্যাপক, গডফ্রিড টোসাইন্ট আবিষ্কার করেছিলেন যে এই অ্যালগরিদমটি ছন্দ তৈরি করতে ব্যবহার করা যেতে পারে। সর্বশ্রেষ্ঠ সাধারণ ভাজক একটি ছন্দে বীটের সংখ্যা নির্ধারণ করে, সমানভাবে বিতরণ করে, এটিকে স্থিতিশীল করে। টুসাইন্ট আরও দেখতে পান যে ইউক্লিডীয় ছন্দগুলি ভারতীয় সঙ্গীত বাদ দিয়ে বেশিরভাগ জাতিগত সঙ্গীত শৈলীর ভিত্তি তৈরি করে।

উদাহরণ স্বরূপ, কিউবান ট্রেসিলো ছন্দ, একটি আট-অংশের দণ্ডের মধ্যে তিনটি বীটে বিস্তৃত, প্রায়ই পশ্চিমা পপ সঙ্গীতে পাওয়া যায়। ইউক্লিডীয় ছন্দগুলি সাধারণত জোড় এবং বিজোড় সংখ্যক বীট এবং বিভাজনকে একত্রিত করে, একটি পরিবর্তন এবং "বাউন্সিং" প্রভাব তৈরি করে যা নৃত্য সঙ্গীতের জন্য আদর্শ। এই ছন্দগুলি বিশেষ সাইটগুলিতে অন্বেষণ করা যেতে পারে যেখানে ছন্দের পরামিতিগুলি সেট করা আছে, যা আপনাকে পলিরিদমের মুগ্ধতা অনুভব করতে দেয়।

এছাড়াও, ইউক্লিডীয় গণনা শুধুমাত্র ব্রাজিলিয়ান বোসা নোভা, তুর্কি আকসাক এবং অন্যান্য জাতিগত ছন্দে নয়, পারমাণবিক পদার্থবিদ্যা, স্ট্রিং তত্ত্ব এবং কম্পিউটার বিজ্ঞানের কণা ত্বরণকারীতেও প্রয়োগ খুঁজে পায়। এটি প্রমাণ করে যে গাণিতিক পদে সঙ্গীতের জটিলতা চোখের মিলনের চেয়ে গভীর হতে পারে।