Rythme euclidien
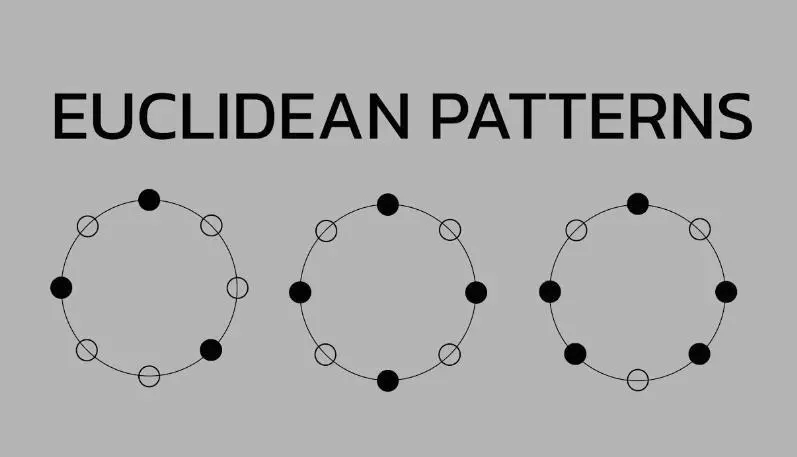
Le lien entre la musique et les mathématiques est connu depuis longtemps, et il ne s’agit pas seulement de math rock. La musique, comme expliqué précédemment, peut être utilisée pour créer des formes sur un plan bidimensionnel, et le rythme et les nombres sont également étroitement liés. Un excellent exemple de cette combinaison est le rythme euclidien, qui démontre la synergie entre les concepts musicaux et mathématiques.
Au 3ème siècle avant JC, l'ancien mathématicien grec Euclide a développé un algorithme pour déterminer le plus grand diviseur commun de deux nombres, basé sur une paire de nombres constitués d'un nombre plus petit et de la différence entre un nombre plus grand et un nombre plus petit.
En 2004, Godfried Toussaint, professeur canadien d'informatique à l'Université de New York à Abu Dhabi, a découvert que cet algorithme pouvait être utilisé pour créer des rythmes. Le plus grand commun diviseur détermine le nombre de battements d'un rythme, uniformément répartis, ce qui le rend stable. Toussaint a également découvert que les rythmes euclidiens constituent la base de la plupart des styles musicaux ethniques, à l'exception de la musique indienne.
À titre d'exemple, le rythme cubain tresillo, réparti sur trois temps dans une mesure de huit parties, se retrouve souvent dans la musique pop occidentale. Les rythmes euclidiens combinent généralement des nombres pairs et impairs de battements et de divisions, créant ainsi une transition et un effet de « rebondissement » idéal pour la musique de danse. Ces rythmes peuvent être explorés sur des sites spéciaux où sont définis les paramètres rythmiques, ce qui permet de ressentir la fascination des polyrythmies.
En outre, les calculs euclidiens trouvent des applications non seulement dans la bossa nova brésilienne, l'aksak turc et d'autres rythmes ethniques, mais également dans les accélérateurs de particules en physique atomique, en théorie des cordes et en informatique. Cela démontre que la complexité de la musique en termes mathématiques peut être plus profonde qu’il n’y paraît.
En musique, une double croche (également connue sous le nom de double croche américaine ou double croche britannique) est un élément musical qui dure la moitié du temps d'une croche (croche)...
Pour comprendre le principe de fonctionnement d'un vocodeur, on peut faire une analogie avec la voix humaine...
La compression parallèle est une technique de mixage puissante qui est activement utilisée dans la musique, mais qui est souvent mal comprise...
Au cinéma (comme George Lucas l'a souligné dans la citation ci-dessus), où le son joue un rôle majeur avec l'image et l'histoire...
Comprendre l'effet de Ratio sur le matériel audio est essentiel pour créer un mixage équilibré et harmonieux...
Quelques conseils simples vous aideront à donner à votre voix un son professionnel. Nous expliquerons comment traiter avec compétence les voix dans un simple éditeur audio et partagerons les effets que les musiciens utilisent...
Il existe une relation étroite entre la musique et la physique dans le domaine du son. Le point de départ de la considération est la soi-disant série harmonique ...
La production audio est une branche de l'industrie musicale qui implique la création de morceaux de musique, leur traitement et leur arrangement...
Il peut y avoir de nombreuses raisons pour lesquelles vous recherchez un outil d'enregistrement en ligne, mais une chose est évidente : avoir la capacité de capturer les sons environnants...
Inscrivez-vous gratuitement et obtenez un projet gratuitement