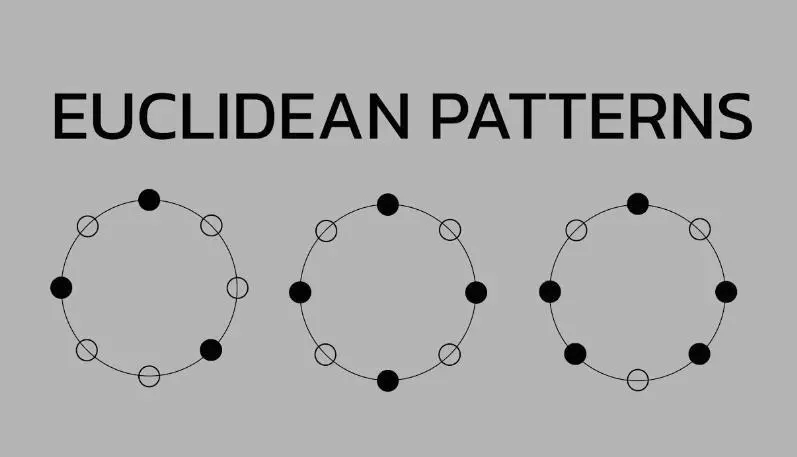
유클리드 리듬

음악과 수학의 연관성은 오랫동안 알려져 왔으며 이는 단지 매스 록에만 국한된 것이 아닙니다. 앞서 설명한 바와 같이 음악은 2차원 평면에 형태를 만들어 내는 데 사용될 수 있으며, 리듬과 숫자 역시 밀접한 관련이 있다. 이 조합의 대표적인 예는 음악적 개념과 수학적 개념 간의 시너지 효과를 보여주는 유클리드 리듬입니다.

기원전 3세기에 고대 그리스 수학자 유클리드는 더 작은 숫자와 더 큰 숫자와 더 작은 숫자의 차이로 구성된 숫자 쌍을 기반으로 두 숫자의 최대 공약수를 결정하는 알고리즘을 개발했습니다.

2004년에 아부다비에 있는 뉴욕 대학의 캐나다 컴퓨터 과학 교수인 Godfried Toussaint는 이 알고리즘이 리듬을 만드는 데 사용될 수 있음을 발견했습니다. 최대 공약수는 리듬의 박자 수를 결정하고 균등하게 분배하여 리듬을 안정적으로 만듭니다. 투생은 또한 유클리드 리듬이 인도 음악을 제외한 대부분의 민족 음악 스타일의 기초를 형성한다는 사실을 발견했습니다.

예를 들어, 8부 마디 내에서 3박자에 걸쳐 펼쳐지는 쿠바 트레실로 리듬은 서양 팝 음악에서 흔히 발견됩니다. 유클리드 리듬은 일반적으로 짝수 및 홀수 비트와 분할을 결합하여 댄스 음악에 이상적인 전환 및 "바운싱" 효과를 생성합니다. 이러한 리듬은 리듬 매개변수가 설정된 특수 사이트에서 탐색할 수 있으며 이를 통해 폴리리듬의 매력을 경험할 수 있습니다.

또한 유클리드 계산은 브라질 보사노바, 터키 악삭 및 기타 민족 리듬뿐만 아니라 원자 물리학, 끈 이론 및 컴퓨터 과학의 입자 가속기에도 적용됩니다. 이는 수학적인 측면에서 음악의 복잡성이 눈에 보이는 것보다 더 깊을 수 있음을 보여줍니다.

DJ이자 음악 프로듀서. 5년 넘게 EDM과 디제잉을 전문적으로 제작해 왔습니다. 피아노로 음악 교육을 받았습니다. 맞춤형 비트를 생성하고 음악을 믹싱합니다. 다양한 클럽에서 정기적으로 DJ 세트를 공연합니다. Amped Studio 블로그의 음악 관련 기사 작성자 중 한 명입니다.

@패트릭 스티븐슨