Öklid ritmi

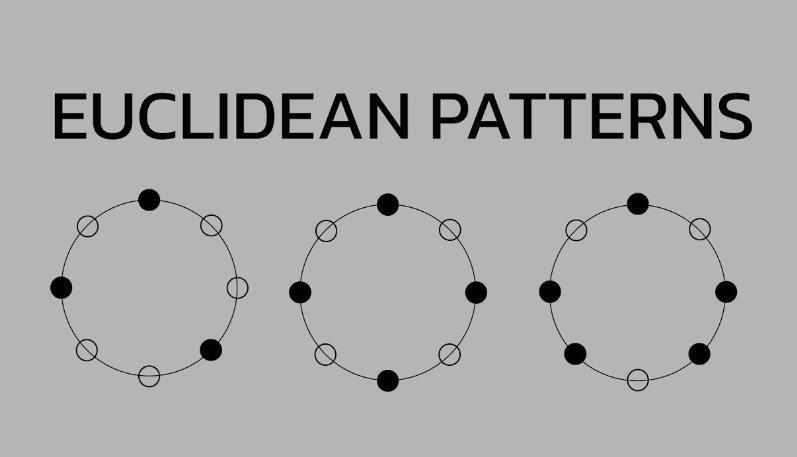
Müzik ve matematik arasındaki bağlantı uzun zamandır biliniyor ve bu sadece matematik rock ile ilgili değil. Daha önce açıklandığı gibi müzik, iki boyutlu bir düzlemde şekiller oluşturmak için kullanılabilir ve ritim ile sayılar da yakından ilişkilidir. Bu kombinasyonun önemli bir örneği, müzikal ve matematiksel kavramlar arasındaki sinerjiyi gösteren Öklid ritmidir.

MÖ 3. yüzyılda, antik Yunan matematikçi Öklid, daha küçük bir sayıdan ve daha büyük ve daha küçük bir sayı arasındaki farktan oluşan bir sayı çiftine dayanarak, iki sayının en büyük ortak bölenini belirlemek için bir algoritma geliştirdi.

2004 yılında, Abu Dabi'deki New York Üniversitesi'nden Kanadalı bilgisayar bilimi profesörü Godfried Toussaint, bu algoritmanın ritim oluşturmak için kullanılabileceğini keşfetti. En büyük ortak bölen, bir ritimdeki vuruşların sayısını belirler, eşit şekilde dağıtılır ve ritmi kararlı hale getirir. Toussaint ayrıca Öklid ritimlerinin Hint müziği dışında çoğu etnik müzik tarzının temelini oluşturduğunu buldu.

Örnek olarak, sekiz bölümlü bir barda üç vuruşa yayılan Küba tresillo ritmi, Batı pop müziğinde sıklıkla bulunur. Öklid ritimleri tipik olarak çift ve tek sayıda vuruş ve bölümü birleştirerek dans müziği için ideal bir geçiş ve "sıçrama" efekti yaratır. Bu ritimler, ritim parametrelerinin ayarlandığı özel sitelerde keşfedilebilir, bu da poliritimlerin büyüsünü deneyimlemenize olanak tanır.

Ayrıca Öklid hesaplamaları yalnızca Brezilya bossa nova, Türk aksak ve diğer etnik ritimlerde değil, aynı zamanda atom fiziği, sicim teorisi ve bilgisayar bilimlerindeki parçacık hızlandırıcılarda da uygulama alanı bulmaktadır. Bu, müziğin matematiksel açıdan karmaşıklığının göründüğünden daha derin olabileceğini gösteriyor.