Euklideszi ritmus

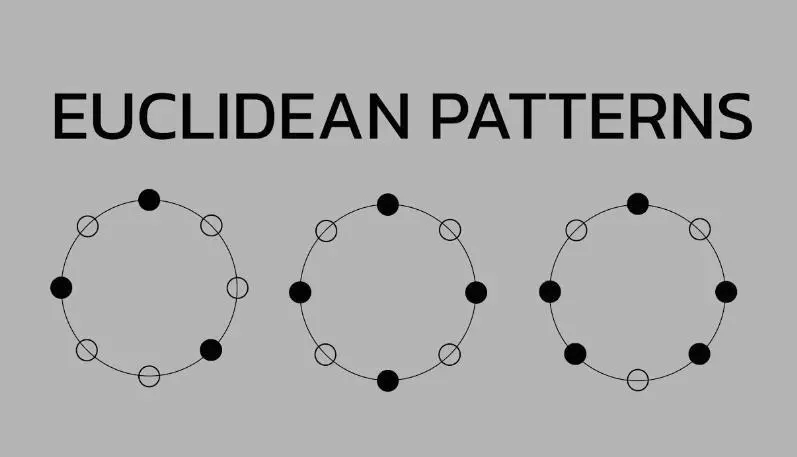
A zene és a matematika kapcsolata régóta ismert, és nem csak a matematikai rockról van szó. A zenével, amint azt korábban kifejtettük, kétdimenziós síkon lehet alakzatokat létrehozni, a ritmus és a számok is szorosan összefüggenek. Ennek a kombinációnak egyik kiváló példája az euklideszi ritmus, amely a zenei és a matematikai fogalmak szinergiáját mutatja be.

A Krisztus előtti 3. században az ókori görög matematikus, Eukleidész kifejlesztett egy algoritmust két szám legnagyobb közös osztójának meghatározására, amely egy kisebb számból, valamint egy nagyobb és kisebb szám különbségéből álló számpáron alapult.

2004-ben Godfried Toussaint, az abu-dzabi New York-i Egyetem egyik kanadai számítástechnika professzora felfedezte, hogy ez az algoritmus használható ritmusok létrehozására. A legnagyobb közös osztó határozza meg az ütemek számát egy ritmusban, egyenletesen elosztva, így stabil. Toussaint azt is megállapította, hogy az euklideszi ritmusok képezik a legtöbb etnikai zenei stílus alapját, az indiai zene kivételével.

Például a kubai tresillo ritmus, amely egy nyolcszólamú ütemben három ütemben terjed, gyakran megtalálható a nyugati popzenében. Az euklideszi ritmusok jellemzően páros és páratlan számú ütemet és felosztást kombinálnak, átmenetet és „pattogó” hatást hozva létre, amely ideális a tánczenéhez. Ezeket a ritmusokat speciális oldalakon lehet felfedezni, ahol ritmusparaméterek vannak beállítva, ami lehetővé teszi, hogy megtapasztalja a poliritmusok varázsát.

Az euklideszi számítások ráadásul nemcsak a brazil bossa nova, a török ​​aksak és más etnikai ritmusokban találnak alkalmazást, hanem az atomfizika, a húrelmélet és a számítástechnika részecskegyorsítóiban is. Ez azt mutatja, hogy a zene összetettsége matematikai értelemben mélyebb lehet, mint amilyennek látszik.