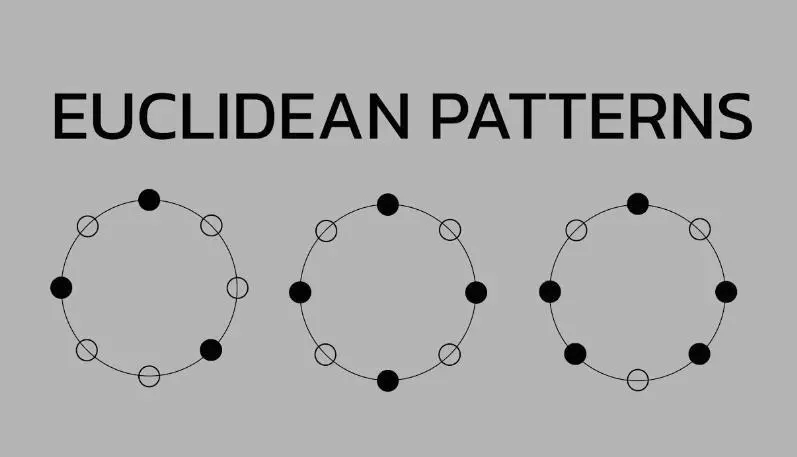
Ritmo euclidiano

A conexão entre música e matemática é conhecida há muito tempo, e não se trata apenas de rock matemático. A música, como explicado anteriormente, pode ser usada para criar formas num plano bidimensional, e o ritmo e os números também estão intimamente relacionados. Um excelente exemplo desta combinação é o ritmo euclidiano, que demonstra a sinergia entre conceitos musicais e matemáticos.

No século III aC, o antigo matemático grego Euclides desenvolveu um algoritmo para determinar o máximo divisor comum de dois números, baseado em um par de números que consiste em um número menor e na diferença entre um número maior e um menor.

Em 2004, um professor canadense de ciência da computação da Universidade de Nova York em Abu Dhabi, Godfried Toussaint, descobriu que esse algoritmo poderia ser usado para criar ritmos. O máximo divisor comum determina o número de batidas de um ritmo, distribuídas uniformemente, tornando-o estável. Toussaint também descobriu que os ritmos euclidianos constituem a base da maioria dos estilos musicais étnicos, com exceção da música indiana.

Por exemplo, o ritmo tresillo cubano, distribuído por três batidas em um compasso de oito partes, é frequentemente encontrado na música pop ocidental. Os ritmos euclidianos normalmente combinam números pares e ímpares de batidas e divisões, criando uma transição e um efeito de “salto” ideal para música dançante. Esses ritmos podem ser explorados em locais especiais onde são definidos parâmetros de ritmo, o que permite experimentar o fascínio dos polirritmos.

Além disso, os cálculos euclidianos encontram aplicações não apenas na bossa nova brasileira, no aksak turco e em outros ritmos étnicos, mas também em aceleradores de partículas na física atômica, na teoria das cordas e na ciência da computação. Isto demonstra que a complexidade da música em termos matemáticos pode ser mais profunda do que aparenta.