Ritmo euclideo

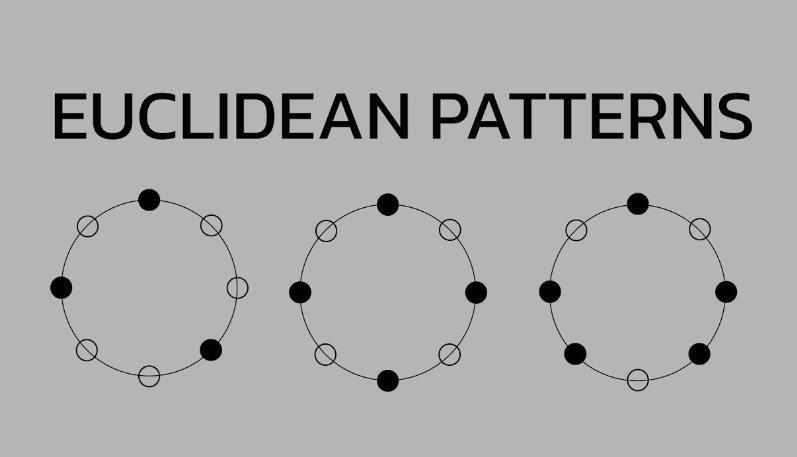
Il legame tra musica e matematica è noto da tempo, e non riguarda solo il math rock. La musica, come spiegato in precedenza, può essere utilizzata per creare forme su un piano bidimensionale e anche il ritmo e i numeri sono strettamente correlati. Un ottimo esempio di questa combinazione è il ritmo euclideo, che dimostra la sinergia tra concetti musicali e matematici.

Già nel III secolo a.C., l'antico matematico greco Euclide sviluppò un algoritmo per determinare il massimo comun divisore di due numeri, basato su una coppia di numeri composta da un numero più piccolo e dalla differenza tra un numero più grande e uno più piccolo.

Nel 2004, Godfried Toussaint, professore canadese di informatica alla New York University di Abu Dhabi, scoprì che questo algoritmo poteva essere utilizzato per creare ritmi. Il massimo comun divisore determina il numero di battiti in un ritmo, distribuito uniformemente, rendendolo stabile. Toussaint scoprì anche che i ritmi euclidei costituiscono la base della maggior parte degli stili musicali etnici, ad eccezione della musica indiana.

Ad esempio, il ritmo cubano del tresillo, distribuito su tre battute all'interno di una battuta in otto parti, si trova spesso nella musica pop occidentale. I ritmi euclidei tipicamente combinano numeri pari e dispari di battiti e divisioni, creando un effetto di transizione e di “rimbalzo” ideale per la musica da ballo. Questi ritmi possono essere esplorati su siti speciali in cui vengono impostati i parametri del ritmo, il che consente di sperimentare il fascino dei poliritmi.

Inoltre, i calcoli euclidei trovano applicazione non solo nella bossa nova brasiliana, nell’aksak turco e in altri ritmi etnici, ma anche negli acceleratori di particelle nella fisica atomica, nella teoria delle stringhe e nell’informatica. Ciò dimostra che la complessità della musica in termini matematici può essere più profonda di quanto sembri.