Euclidean rhythm

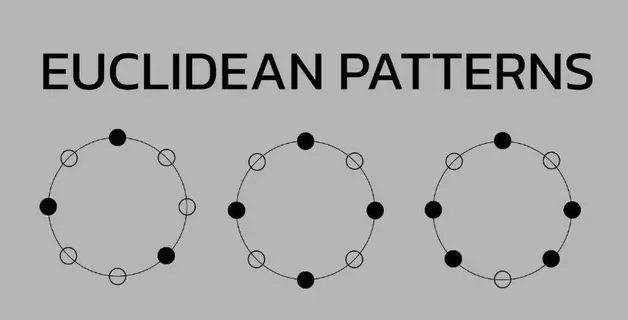
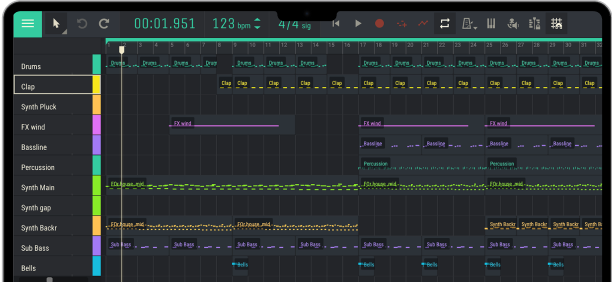
The connection between music and mathematics has long been known, and it’s not just about math rock. Music, as explained earlier, can be used to create shapes on a two-dimensional plane, and rhythm and numbers are also closely related. One prime example of this combination is Euclidean rhythm, which demonstrates the synergy between musical and mathematical concepts.

Back in the 3rd century BC, the ancient Greek mathematician Euclid developed an algorithm for determining the greatest common divisor of two numbers, based on a pair of numbers consisting of a smaller number and the difference between a larger and smaller number.

In 2004, a Canadian computer science professor at New York University in Abu Dhabi, Godfried Toussaint, discovered that this algorithm could be used to create rhythms. The greatest common divisor determines the number of beats in a rhythm, evenly distributed, making it stable. Toussaint also found that Euclidean rhythms form the basis of most ethnic musical styles, with the exception of Indian music.

As an example, the Cuban tresillo rhythm, spread over three beats within an eight-part bar, is often found in Western pop music. Euclidean rhythms typically combine even and odd numbers of beats and divisions, creating a transition and “bouncing” effect ideal for dance music. These rhythms can be explored on special sites where rhythm parameters are set, which allows you to experience the fascination of polyrhythms.

In addition, Euclidean calculations find applications not only in Brazilian bossa nova, Turkish aksak and other ethnic rhythms, but also in particle accelerators in atomic physics, string theory and computer science. This demonstrates that the complexity of music in mathematical terms may be deeper than meets the eye.