音楽における転調
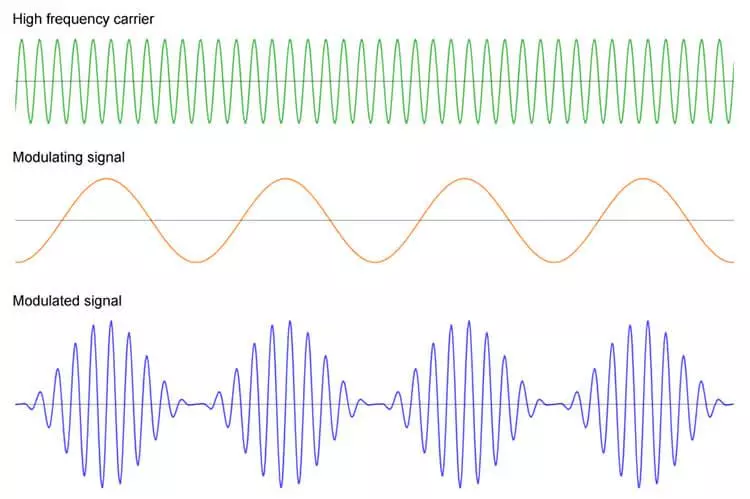
モジュレーションは、あるキーから別のキーへの倍音の移行です。 簡単な例は、次のような A マイナーから C メジャーへの転調です。
イ短調からハ長調への転調
耳は最初イ短調の音構成に配置されていますが、その後、トの調でこの調から切り離されます。イ短調の調の外に他の音が存在しない場合、知覚は、最初に、 g で発生する音、そして第二に、前のキーの音の構成との最大の対応を示します。 この場合はハ長調のキーになります。 変調のより詳細な研究は、最終的には変調の法則に帰着し、それに基づいて音楽作品を倍音分析にかけることができます。
転調では調間の調和のとれた関係が実現されます。 この関係は、音の調和 (協和音) と協和音の調和 (調性) に基づいており、したがって 3 次元の調和を表します。つまり、鍵盤の音色は共通の音色によって調和します。 このハーモニーの通常の表現は、キーの関係です。
音楽における転調
ルート、したがってルートと主音が音楽作品中に長期間にわたって変化する場合、転調が発生しています。 変化が瞬間的であり、新しいトーンが耳に知覚されない場合、それは回避と呼ばれます。
変調には主に 3 つのタイプがあります。
- ダイアトニック;
- クロマティック;
- クロマチック。
次に、それぞれを順番に考えていきます。
ダイアトニック変調
ダイアトニックモジュレーションでは、ソースキーとターゲットキーの間に「リンク」として機能するコードが常に存在します。 このコードは両方のキーで正しいスケールを持っています。 機能的に再考されたので、別の方法で動き続けることができます。 続いて転調コードです。
2 つの異なるキーでスケールされたコードは、まさにそれらのキーの変調コードになる可能性があります。
次の例では、ハ長調からロ短調に変調します。
転調コード(青枠)はEマイナーコードです。 ハ長調の開始キーでは Dp (III 度のコード)、ロ短調のターゲット キーでは s (IV 度のコード) です。 したがって、ハ長調の Dp からロ短調の S に再解釈されます。
再解釈プロセスの後、新しいトニックが元のキー (緑色でマーク) の主音を「忘れる」ように、ターゲット キーを修正する必要があります。 この統合は、ターゲット キーを支配するパスをたどる傾向があり、おそらくターゲット キーのフル ケイデンスを通じて行われます。 変調コードの再解釈は、「≈」という記号で説明できます。
「ダイアトニック」変調という用語の拡張された理解には、ナポリの 6 度の和音 (ナポリタン) などの修正コードも含まれます。 次の例は、トニックを独立したナポリタンに再考することを示しています。 再びハ長調からロ短調への転調。
クロマティックモジュレーション
このタイプの変調は、変調によってキーが変更されることからその名前が付けられました。 スタートキーとターゲットキーに共通するスケールのトライアドは必要ありません。 移行コード (変調コード、青いボックス、以下を参照) は多くの場合区別でき、場合によっては複数存在します。 移行フェーズ中に両方のキーで解釈できるコードが増えるほど (青いボックス、以下を参照)、移行がよりスムーズになります。
理論的には、トーンのタイプは変調において大きな役割を果たしません。 したがって、同じ変調コードを使用してターゲット キーのメジャー バージョンとマイナー バージョンの両方を変調することが可能です。
次の 2 つの例は、ハ長調からイ短調への転調と、ハ長調からイ長調への転調を示しています。 どちらの場合も、対応するターゲット キーのドミナント E メジャー コードは同じ転調コードです。 転調は、短調 (a)) または長調 (b)) で単純に続けることができます。
分析すると、重要な変更が 2 つの「レベル」で記録されます (以下に赤と緑のボックスで示します)。
例 a) ではハ長調の中間ドミナントの最後のコードはスケール (Tp) に固有ですが、例 b) ではそうではありません。 ここで聞こえるのは Tp ではなく、対応するメジャー変種 (TP – ?) であるため、ハ長調レベルとの関係では楕円になります。
変調の可能性の 1 つは、スケールのマイナー コードの「Verduren」(音の変化形)です。 その後、ターゲット キーに対して優勢になります。
この例では、マイナー サブドミナント コードは、A マイナーの最初のキーとその異音 (D マイナー => D メジャー) に従い、ドミナントに変換すると G メジャーへの道が開かれます。 この例では、効果を高めるために、転調コードに 2 番目のコードとしてセブンス コードを追加します。
上の例に従って、下の例では、スケールのメジャーコードを「マイナー化」することで、対象キーのマイナーサブドミナントの関数になります。 次の例は、ハ長調のドミナントの異音の使用を示しています。 結果として得られる G マイナー コードは、D マイナーの新しいターゲット キーのマイナー サブドミナントとして美しく解釈できます。
等調波変調
等価変調では、コードの 1 つまたは複数のトーンを共和的に混合することによってコードが再解釈され、結果として別のキーが変調コードとして生成されます。 これらはドミナントコードです。 これは、ドミナントが複数の解決コードにつながる可能性があることを意味します。 ドミナントは、対応する解決コードのキーに応じて表記が異なります。
特に、変更されたドミナントコードは簡単に再解釈できるため、共和音変調に適しています。
この点で最も汎用性の高いコードは D v です。
この和音の 4 つの音はそれぞれドミナントの 3 番目の音、つまり別のキーの先頭音になるため、それを 4 つの異なるキーに分割し、1 つのキーを他の 3 つのキーに変調することができます。
1. 例: C メジャーから D v を経て A マイナーへ: C メジャーの 9 番目の音「A-フラット」D v は、A マイナーの 3 番目の音「G シャープ」D v になります。
2番目の例:「ハ長調からニ長調、嬰ヘ長調まで:ハ長調の分音「f」Dシャープは第3音「eis」嬰ニ長調、第9音「フラット」は変ニ長調Dvハ長調となります。第5音「G#」Dvヘ長調。
3. 例: ハ長調から変ニ長調、変ホ長調へ: 変ニ長調の 3 番目の音「b」は、変ニ長調の 9 番目の音「ces」になります。
「原始的な」D 7 をモジュレーションに使用して、第 7 倍音を第 3 倍音に変更することもできます。 これにより、補鍵の 5 番目の音をわずかに変更した D v が作成されます。
さらに、高度に変更された 5 度音を含むドミナントは、調和変調に適しています。
他のタイプの変調
ソースキーとターゲットキーの間にモジュレーションコードがないモジュレーションも可能です。 たとえば、ターゲットのキー (ベースの 5 番目の格シーケンス) に到達するまで、5 度圏の 5 度を「歩く」ことができます。 その後、修正する必要があります。
他のトーンも中間局として使用できます。 以下の例では、これはシーケンスとして実行されます。
ハ長調から変ホ長調に転調します。 ハ長調の最初のキーのリズム S-DT が、変ロ長調と変イ長調で繰り返されます (シーケンスされます)。 変イ長調のコードは、変ホ長調のサブドミナントとして解釈されます。
ディンプル変調には特別な効果があります。 この場合、ターゲットキーの機能は、中間コードの「スムーズな」移行に関係なく実行されます。
変調の文学的な例
ダイアトニック変調
バー9以降 ピアノ・ソナタ作品 49 の最初の部分、ルートヴィヒ・ヴァン・ベートーヴェン (1770-1827) より:
ここでは、トニックト短調が変ロ長調のトニックパラレルに転調します。
転調コードは C マイナー コードで、開始キーが G マイナー S、ターゲット キーが B フラット Sp です。
クロマティックモジュレーション
ヴォルフガング・アマデウス・モーツァルト (1756 – 1791) のピアノ・ソナタ ニ長調 KV 576 (狩猟ソナタ) からの展開:
この例の最初の 2 つの転調、59 と 63 小節の間のイ短調から変ロ長調、および 67 と 70 小節の間の変ロ長調からト短調は半音階変調です。
最初のケースでは、決定的なコードは「f」の 7 番目のコード (61/62 小節) で、イ短調では、実際にそれに続く独立したナポリタン (変ロ長調コード、63 小節) への中間ドミナントとして聞こえることができます。 。 このナポリタンも新しい主音であり、61/62 小節の「f」の 7 番目の和音がドミナント機能を持っています。
2番目の場合、根音「d」の性5和音は転調和音(68小節)であり、変ロ長調ではtr(ト短調)の中間ドミナントとなり、新たな主音(70小節)となります。
その後のト短調からイ短調への調の変化は、転調として認定するには短すぎます。 イ短調のトリガーキーはロ短調(m.78)への途中のステーション(中間主音)です。 興味深い移行はロ短調から嬰ヘ短調 (80 ~ 83 小節) で、ドミナントのロ短調 (嬰へ長調コード) が繰り返され、知覚できる中間主音になるまで「下げられ」ます。 さらに調性が変化すると、再び中間局となり、今度はソナタの主調、つまりニ長調に戻ります。 これは、ロ短調の 5 度上の嬰ヘ短調 (T. 86)、ホ短調の最後に達成されたキーに由来しています。
(T. 89)、そして最後にイ長調 (T. 92) でドミナントとしてニ長調が始まります (99 小節)。
ダイアトニックかクロマチックか?
ヨハン・セバスティアン・バッハ(1685–1750)の『フーガの技法』BWV 1080 より、コントラプンクトゥス IV の 80 小節以降。
イ短調からハ長調までの最も美しい転調の 1 つ。
転調コードはヘ長調コードです。つまり、イ短調では tG、ハ長調では S です。
変調コードは両方のキー (tG または S) の音階に固有であるため、ダイアトニック変調となります。 一方、この転調コードを演奏した後は、非常に多くの変更が行われます (mm. 83 以降では、それぞれハ短調とハ長調のダブル ドミナント セブンス コードとドミナント セブンス コードを使用して演奏するため)、クロマチック変調と間違われる可能性もあります。
インデント変調
ルートヴィヒ・ヴァン・ベートーヴェン(1770 – 1827)のピアノ・ソナタ ヘ長調作品 54 の第 2 部の冒頭:
ヘ長調の最初の調からハ長調のドミナントへの移行後(mm.1-21)、イ長調の22小節目で突如として楽章のテーマが鳴り響き、まるで「世界」に運ばれたような気分になります。別世界"。
等調波変調
ルートヴィヒ・ヴァン・ベートーヴェン(1770–1827)の『バガテル ト短調 作品 119 第 1 番』からの抜粋。
ここでは変ホ長調からト短調に転調されています。 転調コードは、33 小節の 3 拍目にある青色の枠で囲まれたコードです。耳は最初、このコードを変ホ長調のサブドミナントに対する中間ドミナントとして解釈します。 その場合、転調コードは 7 番目の音として「半音フラット d、D 2」で記譜する必要があります (参考ノートを参照)。 ベースの「Eを半音下げたE 2」がコードのルートになります。 ベートーベンは「半音フラット d、D 2」の代わりに「C シャープ」を記譜するため、ルート音「E を半音フラットにした E 2」は、短縮されたダブル ドミナント セブンス コードの低変 5 度になります。ト短調で。 (欠けているルートは「a」です。)これはドミナントのト短調 6 分の 4 和音で解決されます。
調和の理論
通奏低音 - ステップの理論 - 機能の理論 - ジャズとポップ ミュージックのコード記号。
フィギュアドベースは理論ではありませんが、ステップ理論の前提条件を作成したため、この章である程度詳しく説明します。 これは理論ではありません。フィギュアドベースの目的は、コードを特定の方法で記譜することであり、コードのさまざまな表現を説明することではないからです。
ステップ理論
個々のコードの構造を認識し、コード内のトーンの品質を決定したいと考えています。
機能理論
ステップ理論のスキルが含まれており、コード間の関係も扱います。
説明の試みが異なるため、2 つの理論の間には異なる見解があります。 特定の問題を説明する際、それぞれに長所と短所があります。
フィギュアドベースと同じ理由で、ジャズやポピュラー音楽のコード記号は理論ではありません。 しかし、これは現代の記録に対応する形式であるため、ここでさらに詳しく検討します。
変調則
変調の概念から次の法則が導き出されます。
- 調性は、その調性の音構成にのみ属することができるトーンの存在によって形成されます。
- 調性が形成される前(調性が無関心な状態)では、転調(=別の調性への移行)は不可能です。
- 調性は、この調性の調性構成に含まれないトーンの出現によって放棄されます。
- いくつかのキーで発生する可能性のある調性のままサウンドが放置され、そのどれもが左のキーとの大きな関係によって区別できない場合、調性の無関心が発生します。
- その間に生じた音の無関心は、音を追加することで直接解決でき、その助けを借りて、音の最大一致の法則に従って新しい音のアイデンティティが生まれます。
- その間に生じた音の無関心は、音によって間接的に解決することができます。音は、後から考えると、知覚に 2 つの変調のシーケンスを提示し、全体として最大の音の対応を明らかにします。
- その間に生じた音の無関心は、音によって間接的に解決することができます。音は、後から考えると、知覚に 2 つの変調のシーケンスを提示し、全体として最大の音の対応を明らかにします。
- どのキーでも発生しないキーから音が出る場合、この無調音の結果として左のキーとの接続が失われます。
- 放棄されたキーとの接続が失われると、最初はいかなる変調も排除され、新しい構成が必要になります。
これらの法則を考慮することは、音楽作品の倍音分析を正しく行うために必要な条件です。 一般に受け入れられている変調の概念は、再解釈という誤った概念で機能します。
変調の原理からこれらの法則を導き出し、音例を使用したより正確な表現は、調性音楽の第 3 章に記載されています。