Subdominant and dominant

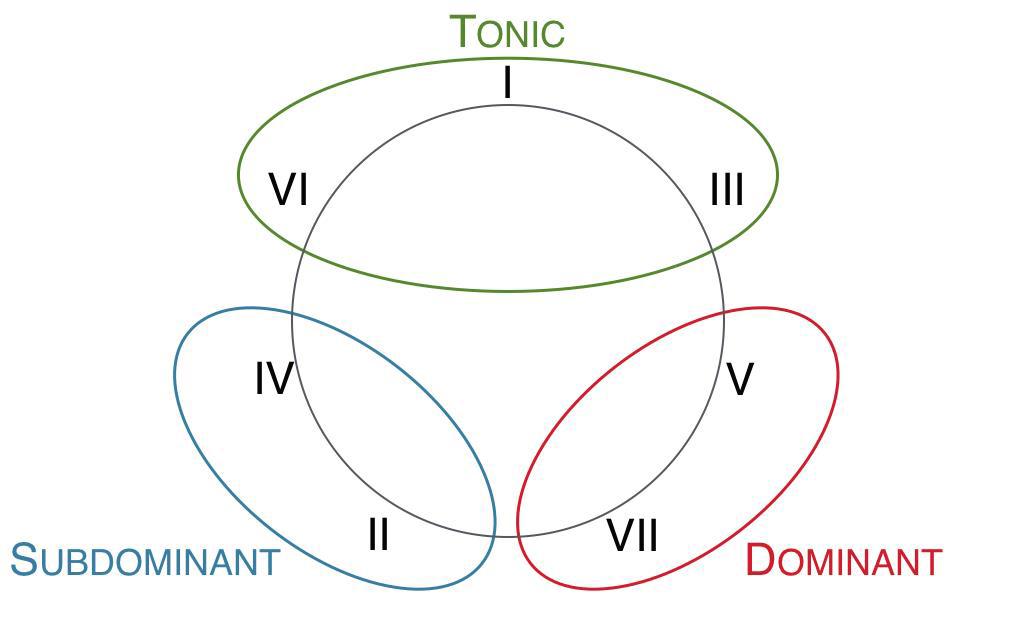
In music theory, the subdominant is the fourth degree in both major and minor modes. The term is also applied to a chord based on the fourth scale degree. The subdominant is one of the three key tonal functions, along with the tonic and the dominant. In analytical notation, it is denoted by the Roman numeral IV or the Latin letter S.

A brief description

Jean-Philippe Rameau, in his treatise “A New System of Theoretical Music” (1726), introduced the term “subdominant” as an analogue to the “dominant”. Rameau defined these terms not as tonal functions, but as sounds in the musical scale that are a fifth higher (dominant) or lower (subdominant) than a single note. He also applied the term “subdominant” to a chord based on the corresponding degree. Rameau described the subdominant plagal cadence (as an “imperfect cadence”) and the dominant authentic cadence (as a “perfect cadence”), pointing to them as characteristic chord progressions in tonal music.

Hugo Riemann made significant contributions to music theory by introducing the concept of the subdominant as a tonal function and introducing the notation S for it. In later theoretical work, second and sixth chords and seventh chords, as well as their inversions, were classified as part of the “subdominant group” “. Typical examples of the subdominant include: the second-degree sixth chord (a subdominant with an added sixth instead of a fifth), the second-degree quintessex chord (a subdominant with an additional sixth, known as Rameau’s sixte ajoutée, that is, “added sixth”), the Neapolitan sixth chord (a minor subdominant with a lower sixth instead of fifths) and others. The main characteristic of the subdominant function is the presence of a sixth scale degree in the chord, which tends to move down towards the fifth of the tonic.

Reception

Rudolf Reti describes the subdominant function in music as a key creative component of composition. He notes that although the I-V-I sequence is a natural phenomenon, creativity occurs when the first degree (I) leads not to the fifth (V) but to another melodic-harmonic element, designated x. Yuri Tyulin emphasizes that the subdominant has a weaker attraction to the tonic compared to the dominant, which he explains by musical-acoustic principles, following Rameau and Riemann. According to his theory, the tonic is derived from the subdominant, just as the dominant is derived from the tonic, referring to the fact that the fifth tone is the second overtone in the natural scale. According to Yuri Kholopov, the subdominant has a particularly gentle attraction to the tonic, since the main tone of the tonic is included in the consonantal core of the subdominant. However, Lev Mazel puts forward the opposite opinion, arguing that melodic gravity plays a leading role and is supported by acoustic laws. In his concept, the subdominant acts as a harmonic element directed from the tonic, in contrast to the centripetal dominant.